6. Results¶

When the communication between the USRPs was established, the transmitted constellation below was obtained.

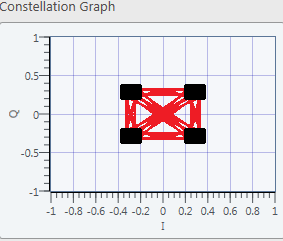
Figure 6.1 Transmitted Constellation

Using the reshape function in LabVIEW, the symbol rate of 62500 symbols/sec is multiplied by the number of samples per symbol, since the demodulator dunction assumes that this would be the sample rate of the input waveform. The received constellation is shown below. The $BER$ in this case is, evidently, 0.

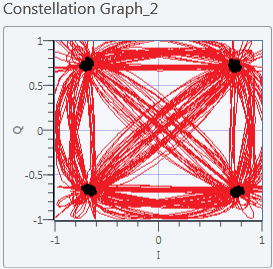
Figure 6.2 Received Constellation without AWGN

The constellation on Figure 6.3 was obtained when adding AWGN, for a target $E_b/N_0$ (received $E_b/N_0$) of 5.The constellation will vary as the values of $E_b/N_0$ vary, making it either noisier, or making it resemble a noiseless channel.

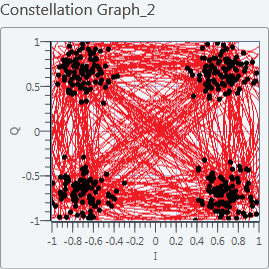
Figure 6.3 Noisy Constellation

With AWGN, the $BER$ is calculated, then compared to the theoretical one, obtaining a $BER$ vs $E_b/N_0$ graph like the one depicted below in Figure 6.4. It can be seen that the simulated $BER$ follows, as expected, the same behavior as the theoretical $BER$, validating simulated results

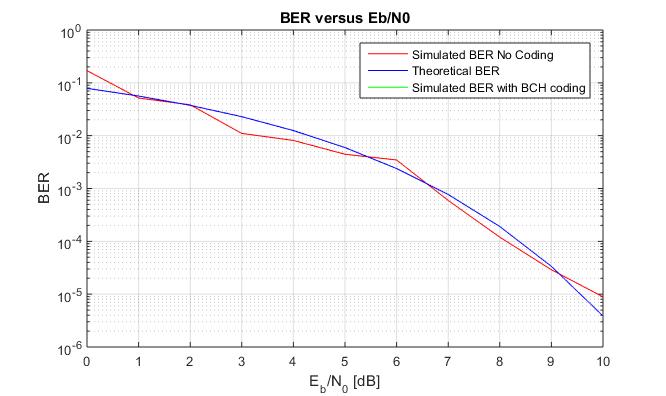
Figure 6.4 BER vs Eb/No without coding

The $BER$ is also calculated for a the BCH code(31,15,3) and for BCH code(7,4,1), and compared to the simulated $BER$ without coding. The resulting graphs presented below

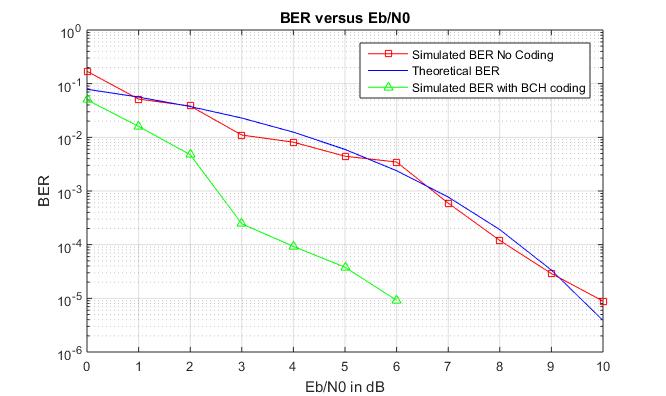
Figure 6.5 BER vs Eb/No with BCH code(31,16,3) coding

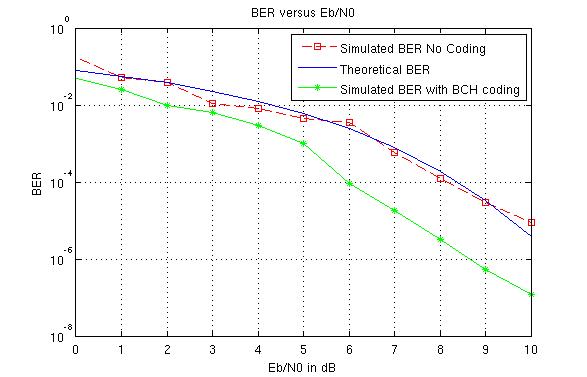
Figure 6.6 BER vs Eb/No with BCH code(7,4,1)

Both codes have roughly a rate of 1/2, but it is observed that there is greater improvement for BCH code(31, 15,3) since this code can correct more errors in a given bit length (simulated bit stream is of length 3000 bits with coding) than BCH code(7,4,1). For BCH code(31, 15,3) there is a coding gain of 3,5dB for a $BER=10^-5$ while for BCH code(7,4,1) the coding gain for the same $BER$ is of 2dB.